After observing O Sensei, the founder of Aikido, sparring with an accomplished fighter, a young student said to the master, “You never lose your balance. What is the secret?”
“You are wrong,” replied O Sensei. “I am constantly losing my balance. My skill lies in my ability to regain it.”

Balance in Martial Arts
When you think about balance and martial arts, you might imagine a familiar image of a person standing on one leg and kicking with another, body perfectly poised to provide counterweight to the kicking leg. This is only a small part of what balance really means as one of the fundamental principles in martial arts.
Balance, posture and stability are the first things a martial art student learns. Learning just a technique without paying attention to proper alignment of the body is not going to get you anywhere. The act of breaking your opponent’s balance (often called kuzushi, especially in judo) is at the center of almost all techniques.
“Breaking balance” doesn’t mean that the attacker is falling down, it means their body’s structure is not stable. Physics talks about objects in stable or unstable equilibrium. Stable equilibrium means that small pushes may displace the object a bit, but then it returns to its original position. If you push an object in an unstable equilibrium even a little, it is displaced permanently and cannot go back. Same thing happens with the body – if you manage to make the opponent lose their body’s stability, your next movement can bring them down. Strength is not necessary for a successful technique if you break your opponent’s balance, but keeping your own balance and stability with every movement is essential.
Physics is not all there is to balance in martial arts. Mental balance and stability are also extremely important, as well as the mind-body balance. You need to be concentrated on your body center and at the same time attuned to everything that happens around you, feel rooted to the ground and be ready to move at any moment.
When somebody tries to attack you forcefully, the very act of the attack makes them unbalanced, and the more raw strength and tension they are putting into the attack, the more out of balance it makes them. A trained aikido practitioner can redirect the attacker’s energy to make them throw themselves, while the defender is staying physically and mentally balanced the whole time. The same can happen with a verbal attack. The skill of deflecting a verbal attack is often called “the mental aikido”. The key point here is to stay balanced and calm, and not meet anger with anger – that would be an equivalent of meeting the blow with a direct blow, which won’t end well if you’re up against someone stronger than you. Serious budo students practice balance not only on the mat, but in all areas of their lives.
Balance in Algebra and Beyond
A notion of balance is often invoked when we’re studying math equations. Two sides of an equation are balanced like two sides of a scale, and as we add or subtract weights, the balance doesn’t change as long as we’re doing the same on both sides. More generally, we can do the same operations on both sides of the equation, as long as they are allowed, and still get a balanced equation. It is important to remember that the new equation doesn’t necessarily have the same roots as the original one – for example, if you square both sides of x-2=3, you’ll end up with the equation (x-2)^2 = 9, which has two roots instead of one. We say that the second equation follows from the first (the balance is kept), but not the other way around.
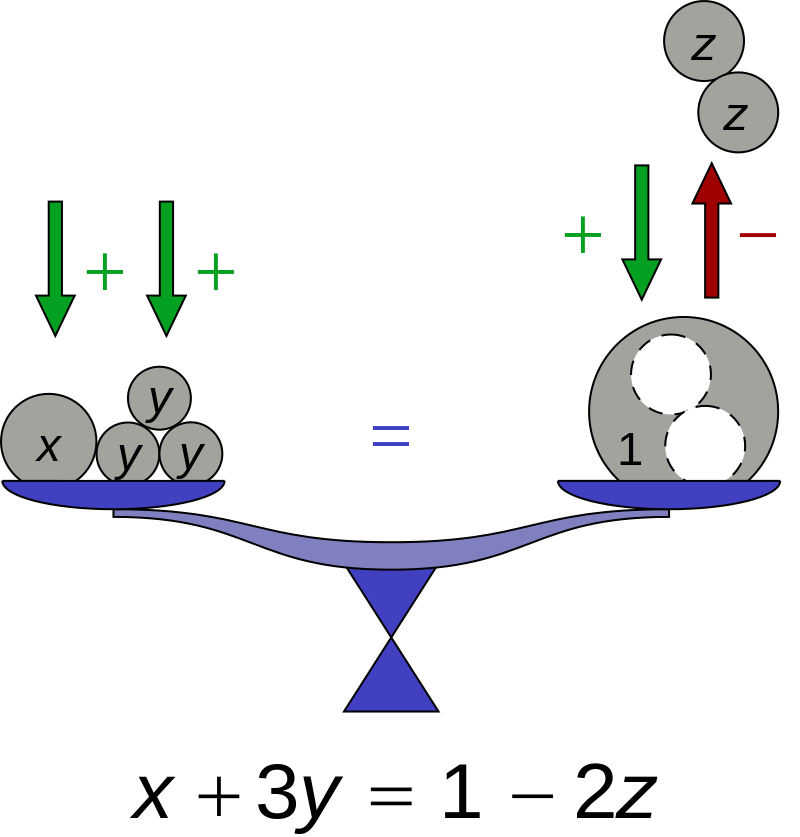
We can also talk about balance as related to centers of gravity, geometrical centers of objects, as well as means and averages. I already discussed triangle centers as part of the Geometry of Aikido, and I’ll leave the rest until the next post.
Balance-related Puzzles
There are a number of cool math problems related to scales and balance. Let’s look at a couple.
Here’s a well-known puzzle. Try to solve this before viewing the solution below.
You have three coins and a scale but no weights. All coins are identical except one which is counterfeit and lighter than others, but looks exactly the same. How would you find out which coin is counterfeit, if you’re only allowed one weighing?
View solution
Put any two coins on two sides of the scale. If one of them is lighter, it is counterfeit. If they are of equal weight, the the counterfeit coin is the one that wasn’t on the scale.
Now let’s say you have 9 coins and can weigh them twice, how would you go about finding the counterfeit coin?
View solution
Divide the coins into three stacks of three coins each, and compare the weight of any two stacks. Then the stack that contains the counterfeit coin will be lighter than any of the others. Using the same method as in the previous problem, you can weigh two of the stacks to find the lighter stack. Then you weigh two coins from this stack to find the counterfeit coin, exactly as before.
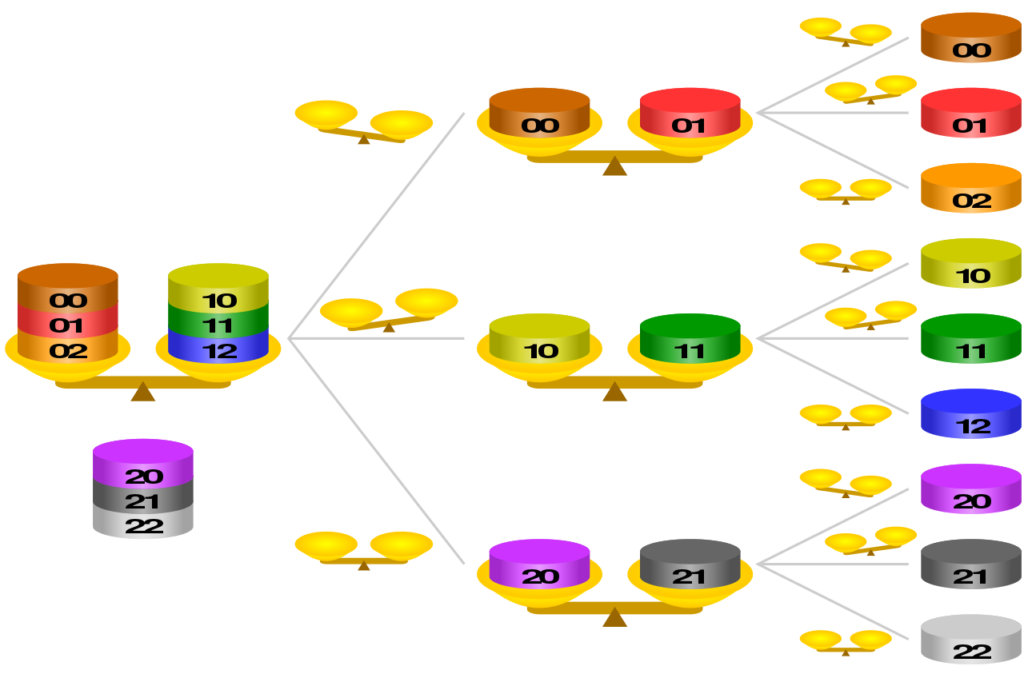
You can probably guess that 27 coins will require 3 weighings, and 3^n coins – n weighings. There are many other versions of this problem. In some of them you don’t know whether the counterfeit coin is lighter or heavier that the rest, or even if there is a counterfeit coin. In this case, you’ll need two weighings for three coins. Try to figure it out! For more coins, the solutions will be much more complicated than before.
Here’s another balance-related problem. Suppose we build a tower of uniform rectangular blocks in the following way: put the first block on the edge of a table, the next one on top of it but shifted a bit over the edge of the table, the third one shifted even more, and so on. How far away from the edge of the table can the tower go without falling down? (The structure won’t fall if its center of mass is over the table.)
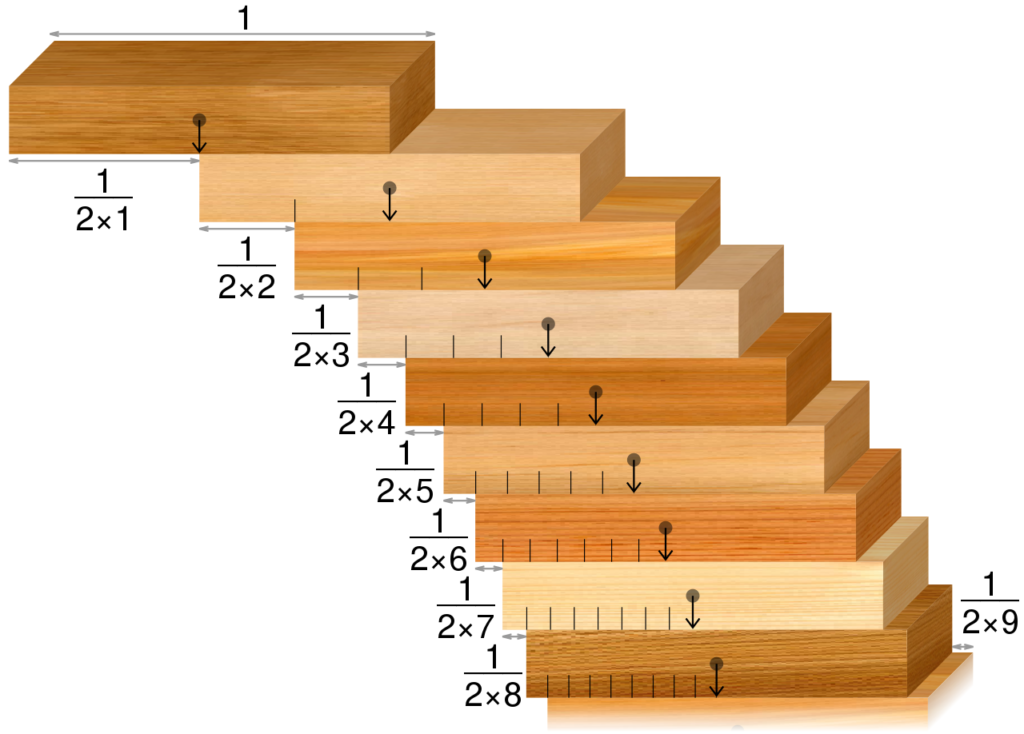
The answer may surprise you. It turns out that the maximal overhang can be achieved if the top block is shifted 1/2 its length from the next one, which is shifted 1/4 its length from the next, then 1/6 and so on. The resulting overhang for n blocks is 1/2+1/4+1/6+…+1/{2n}. This is one half of a partial sum of the aptly named harmonic series. 1+1/2+1/3+1/4+…. The harmonic series diverges, meaning that the partial sums grow withour boundary as the number of terms increases. So the overhang, with a large enough number of blocks, can be made as large as we want. Of course, the height of the tower may be prohibitively huge!
Going back to the more philosophical level, it’s also very important in math, as in all areas of life, to find the right balance between memorizing and understanding, creativity and practice, kata and waza. Achieving balance and stability in your life doesn’t mean freezing in place or losing flexibility, it means you can deal with anything life throws at you while staying centered and light on your feet. I don’t think I’m there yet, but let’s keep trying!
Learn more
If you are a diehard puzzle enthusiast, these links are for you:
Coins and Logic -Tanya Khovanova’s article on coin problems and their surprising relationship to knights-and-knaves puzzles.
