Ueshiba Morihei (O-Sensei), the founder of aikido, wrote:
“The body should be triangular, the mind circular. The triangle represents the generation of energy and is the most stable physical posture. The circle symbolizes serenity and perfection, the source of unlimited techniques. The square stands for solidity, the basis of applied control.”
The three basic shapes of geometry have deep meaning in Shinto religion, where much of budo philosophy originates. These forms have been associated in Shinto with a number of triads from physical and spiritual worlds, like Sun, moon, and stars; gas, liquid, and solid; mission, life, and destiny; rice, water, and salt.
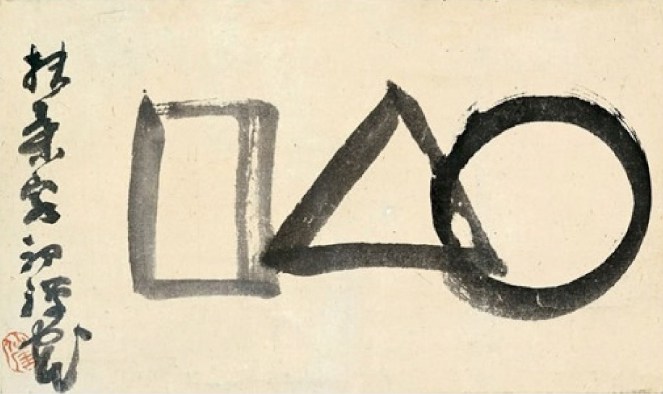
A Triangle
The basic stance of aikido, called hamni, is a triangular stance, where feet are turned roughly perpendicular to each other, and the weight of the body points down to the center of this triangle. This is a stable initial position, and as you move, you shift to a different triangle, always keeping your balance in the center. Also the diagonal step away from the centerline, avoiding a direct attach, may be represented by a triangle.

Since we’re talking about geometry, what exactly is meant here by the center of a triangle? A triangle, as opposed to a circle, has many possible definitions of a center. Here are a few of them:
- Incenter: center of the inscribed circle (the largest circle contained inside a triangle)
- Circumcenter: center of the circumscribed circle (the circle that passes through all vertices of the triangle)
- Orthocenter: point of intersection of the three altitudes (lines starting at vertices and perpendicular to the opposite sides)
- Centroid: point of intersection of the three medians (line segments joining vertices to the midpoint of the opposite sides)
You might have seen these in a geometry class, but did you know there are more than 32,000 different triangle centers? This is because the formal definition of a triangle center is any point that is invariant under similarity transformation. That is, if you move, reflect, or stretch a triangle, its center ends up in a point, which happens to be the same kind of center for the new triangle. Here are a couple of examples of more exotic triangle centers:
- Fermat point: Point that is the smallest possible sum of distances from the vertices.
- Nine-point center: Center of the nine-point circle – a circle passing through the midpoint of each side, the foot of each altitude, and the midpoint between the orthocenter and each vertex.
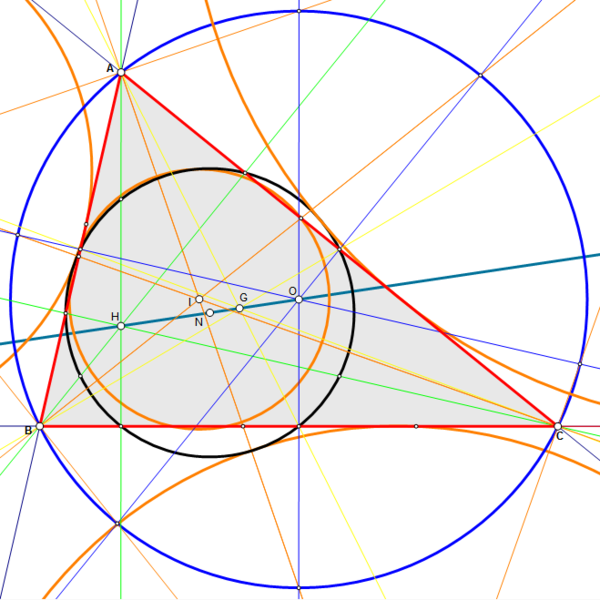
I’m not sure which center we’re talking about in aikido, but I suspect it’s the centroid, which also happens to be the center of mass of the triangle, or the point at which a uniformly thick triangular plank can be balanced.
A Square
A square in aikido represents solidity and stability, movement back and forth, meeting the attack head-on.
You’ll find squares in all areas of math. The most well-known relation between triangles and squares, as well as geometry and algebra, is the Pythagorean theorem:
\[ \mathbf{a^2 + b^2 = c^2}, \]where \(a, b, c\) are sides of a right triangle.
A triple of integer numbers \(a, b, c\) for which this equation is true is called a Pythagorean triple. The most simple and famous example is the triple \((3, 4, 5)\).
Pierre Fermat, famous for not proving Fermat’s Last Theorem (that this equation cannot hold for cubes or any other integer powers), also did not write down the proof of Fermat’s theorem on sums of two squares. It states that an odd prime number can be expressed as a sum of two squares:
\[ p = a^2 + b^2,\]
if and only if \(p = 4n + 1\) (has a remainder 1 when divided by 4). From this it’s possible to find a condition for any positive integer to be a sum of two squares.
The squares don’t stop there. There’s a Legendre’s three-square theorem which gives us the numbers that can be expressed as a sum of three squares, and Lagrange’s four-square theorem, about the sum of (you guessed it) four squares. However, you might not have guessed that every single positive integer can be expressed as a sum of four squares.
A Circle and a Spiral
The circular and spiral motion is behind most of the aikido techniques. It is important that movements come from the center of your body which usually lies a little above the hips. When you connect to your partner’s center and turn around your center in a circular motion, you end up moving your partner. Making this circle a spiral, you can either take your partner down to the ground (downward spiral), or lift their center of gravity up, making it easier to move them (upward spiral).
Unsurprisingly, there are many types of spirals in math. Well-known examples include:
- Archimedean spiral, which you get if you move a point at a constant speed away from a fixed point along a line that moves around this point with a constant angular velocity. Or, in fact, every time you roll a rug.
- Logarithmic spiral in which the distance from the center increases exponentially with the angle. It was also called spira mirabilis by Jakob Bernoulli, a 17th century mathematician who studied it. Bernoulli was so fascinated by this spiral he wanted it engraved on his tombstone together with a motto Eadem Mutata Resurgo meaning “I shall arise the same though changed”. Unfortunately, the stone carvers weren’t mathematicians, and his tombstone features an Archimedean spiral instead. Logarithmic spiral appear in a lot of places in nature, from pinecones to spiral galaxies.
- A 3-d spiral that looks like a coil spring is called a helix. The most well-known use of this word is of course a double helix of the DNA.
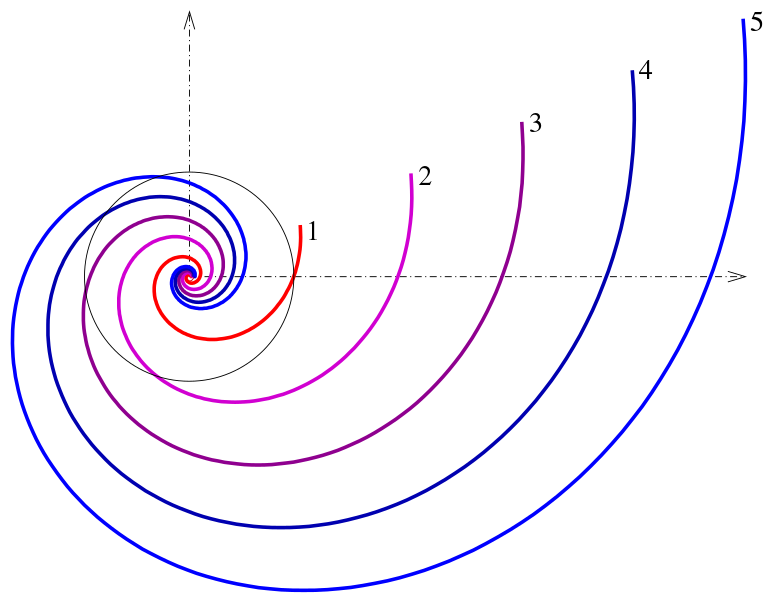
In aikido, we create a kind of a helix but its radius doesn’t stay the same – we not only take the partner down but also bring them towards our center for a pin or extend outward so they can roll. This is a type of a conic spiral.
Learn More
Zen and Shinto 4: Circle, triangle, square
Professor Clark Kimberling’s Encyclopedia of Triangle Centers
