For the interminable months of the pandemic, our dojo was closed, and classes were held on Zoom. You’ll understand why this is not really a satisfying way to do aikido, but some of the ideas for training alone were quite useful. One was to have an imaginary partner, going through a technique while imagining not empty space but a human being in front of you. That got me thinking about other ways we use imaginary entities, and math is of course the first thing that comes to mind.
In fact, all math is about imaginary entities of a sort. The number 2 doesn’t exist in reality; our mind abstracted it from two people, two stones, two days, and a huge number of other pairs. Unless, of course you’re a Platonist – a philosopher who, following in the footsteps of Plato, affirms that abstract mathematical entities have some kind of real existence. However, I’m not going to dive here into the philosophy of mathematics, it can make your head spin very fast in several directions at once, so let’s stick with this simple notion that whole numbers 1,2,3,… are abstractions of physical quantities.
From here, mathematicians added more and more types of numbers, and until a point they all made physical sense. Negative numbers come from moving in a different direction, real numbers from measurements of continuous quantities like a plot of land. You can’t really get irrational numbers by imprecise measurements, but they appear naturally as a diagonal of a square, or a ratio of a circle’s circumference to its diameter. However, when mathematicians started thinking about algebraic equations, they invented a new type of numbers, that they actually called imaginary because on the surface of it they had no physical sense altogether.
While many mathematicians contributed to our understanding of complex numbers, starting with Gerolamo Cardano in the 16th century, the term “imaginary number” was coined by René Descartes in 1637. Carl Friedrich Gauss, who introduced the term “complex number”, didn’t like the word “imaginary”. He wrote: “If one formerly contemplated this subject from a false point of view and therefore found a mysterious darkness, this is in large part attributable to clumsy terminology. Had one not called \( +1, −1, \sqrt{−1} \) positive, negative, or imaginary (or even impossible) units, but instead, say, direct, inverse, or lateral units, then there could scarcely have been talk of such darkness.” It was too late, however, and the term stuck.
Of course, mathematicians don’t just invent new numbers out of the blue. They need to serve some purpose, and fit together with the previously known math facts. Complex numbers arose as solutions of polynomial equations. The simplest imaginary number \(i\) is the square root of \(-1\), or the solution of an equation \( x^2+1=1\). Other imaginary numbers are the multiples of \(i\). Complex numbers are sums of real and imaginary parts, \(a + bi\). We normally represent real numbers geometrically as a line, and complex numbers as points on a plane with two coordinates, \(a\) and \(b\). With these numbers, every polynomial of \(n^{th}\) degree has exactly \(n\) complex roots, which is quite convenient. However, this is far from the only reason mathematicians are “imagining” them.
Complex numbers make a lot of things simpler and make seemingly unrelated things come together, like exponents and trigonometric functions. The physicist Richard Feynman called the following formula (known as Euler’s formula) “the most remarkable formula in mathematics”.
\[ e^{ix} = \cos{x} + i\sin{x} \]From this, we get a famous formula uniting all the most important constants in mathematics:
\[ e^{i\pi} + 1 = 0 \]I used to think math was no fun,
‘Cause I couldn’t see how it was done.
Now Euler’s my hero,
For I now see why 0
Equals e to the pi i + 1.
– Paul Nahin, author of the book Dr. Euler’s Fabulous Formula
Is it just a pretty little formula or can we actually get some use out of it? The surprising fact is that complex numbers make many things significantly less complex. If you struggled with remembering trigonometric formulas like sine of a sum, they can easily be derived using complex exponents.
Riemann zeta function
This was just a taste of how powerful functions of complex variables can be in math. This includes unexpected fields like geometry and especially number theory. The number theory studies those most non-imaginary numbers of all – the integers, but stepping outside into the world of complex numbers opens a whole new realm of possibilities for studying integers. For example, let’s look on the famous Riemann zeta function, starting with the following series studied extensively by Euler in the 17th century – an infinite sum
\[ \zeta(s) = \sum_{n=1}^{\infty}\frac{1}{n^s} = 1 + \frac{1}{2^s} + \frac{1}{3^s} + … \]Euler proved a surprising result connecting this series to prime numbers (the product on the right is taken over all prime numbers).
\[ \sum_{n=1}^{\infty}\frac{1}{n^s} = \prod_{p\ prime} \frac{1}{1 – p^{-s}} = \frac{1}{1 – 2^{-s}} \cdot \frac{1}{1 – 3^{-s}} \cdot \frac{1}{1 – 5^{-s}} \cdot \frac{1}{1 – 7^{-s}}… \]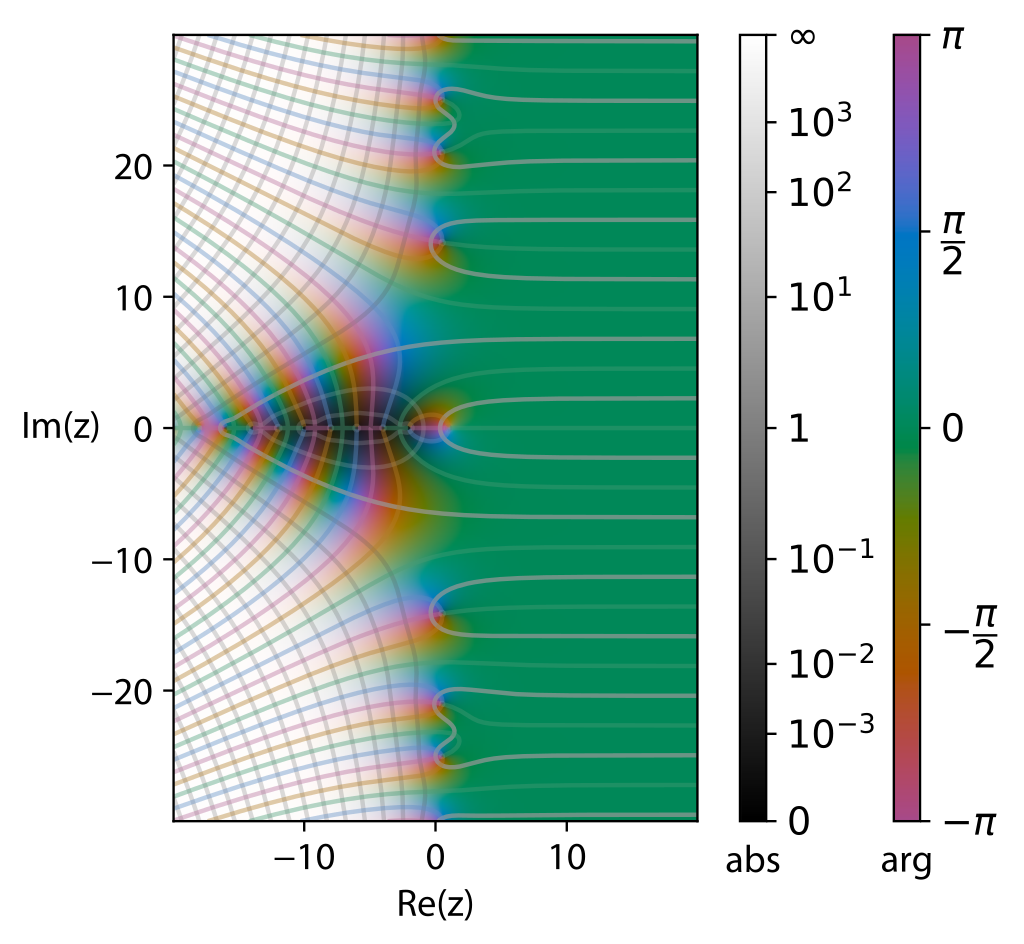
After more than a century, Bernhard Riemann extended this series to a function \(\zeta(s)\) of a complex variable. He also extended its connection to prime numbers, proving that we can calculate the distribution of prime numbers (for any number, counting the number of prime numbers less than this number) if we know where \(\zeta(s) = 0\). The Riemann hypothesis states that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part \(1/2\). It is considered one of the most important unsolved problems in all of mathematics. In 2000, the Clay Mathematics Institute included it in its list of Millennium Prize Problems – seven important unsolved problems in mathematics. A mathematician who solves any of these problems will receive a prize of a million dollars. I’m afraid this may be the hardest way ever to earn a million dollars, but also a sure way to get your name into math textbooks. If one of my readers eventually proves the Riemann hypothesis, don’t forget to mention this site in your prize acceptance speech!
Complex numbers play a great role in many areas of pure and applied science, like quantum mechanics and electrical engineering. The device you’re reading this right now would probably not exist without the invention of complex numbers. Invention… or discovery? In fact, Freeman Dyson in his 2009 article “Birds and Frogs” (worth reading for many other reasons) eloquently argues that complex numbers are the most “natural” numbers of all.
All through the nineteenth century, mathematicians from Abel to Riemann and Weierstrass had been creating a magnificent theory of functions of complex variables. They had discovered that the theory of functions became far deeper and more powerful when it was extended from real to complex numbers. But they always thought of complex numbers as an artificial construction, invented by human mathematicians as a useful and elegant abstraction from real life. It never entered their heads that this artificial number system that they had invented was in fact the ground on which atoms move. They never imagined that nature had got there first.
Julia Sets
So far we talked a lot about simplifying things with complex numbers, but if you want to get some real complexity out of them, you can start with a very simple equation to get a Mandelbrot or Julia set. I’m especially partial to Julia sets because, you see, my name is Julia – although in case of Julia sets, it’s not a first but a last name of a French mathematician Raoul Julia! This is how a Julia set is defined:
Let \( f(z)\) be a function of a complex variable. For every point \(z_{0}\) on the complex plane we can create a sequence of iterations \(z_{1} = f(z_{0}), z_{2}=f(z_{1})\) and so on. This sequence is called an orbit of \(z_{0}\). It can eventually converge to a point, or repeat itself in a cycle, or do neither and behave in an unpredictable, chaotic manner. The set of all points with chaotic orbits is called the Julia set for the function \(f\).
For some functions their Julia sets are fractal. The most well-known is the family of functions \(f(z) = z^2 + c\), where c is a complex number.

We started to “imagine” numbers and ended up with the gamut of surprising applications, from quantum mechanics to pretty fractal pictures. Imagination is a powerful tool of understanding and changing the world and yourself. Going back to martial arts, I discovered that just imagining myself doing techniques in my mind can be very useful in understanding and remembering them. That was before I found out that, according to neuroscience, the same brain circuits light up when imagining movements as when actually doing them. This doesn’t mean you can substitute doing exercise in your head while lying on a couch for actual exercise or martial arts training!
Imagination can also be a force for the bad. If you keep imagining crimes or frauds where there was none, you will only increase the amount of crime, fraud and suffering in the world. I hope you will use your imagination as a creative force for good, and make imaginary numbers your friends!
